Difference between revisions of "CH391L/HiddenMarkovModel"
From Marcotte Lab
< CH391L
(→Viterbi Algorithm) |
|||
| Line 1: | Line 1: | ||
== Viterbi Algorithm == | == Viterbi Algorithm == | ||
| − | This is an 'dishonest casino' example from Durbin, et al. 'Biological Sequence Analysis' book. A casino used two types of dice: one is a 'fair' one that has equal chance to all six numbers, and the other is a ' | + | This is an 'dishonest casino' example from Durbin, et al. 'Biological Sequence Analysis' book. A casino used two types of dice: one is a 'fair' one that has equal chance to all six numbers, and the other is a 'loaded' one that has high chance of number 6 than the others. We have a sequence of dice numbers from the casino, and want to estimate when a dealer exchanged the dice. |
We assume that the Hidden Markov Model of this example as below: | We assume that the Hidden Markov Model of this example as below: | ||
| + | |||
http://www.marcottelab.org/users/CH391L/FromTA/HMM_dice.png | http://www.marcottelab.org/users/CH391L/FromTA/HMM_dice.png | ||
| + | |||
| + | As you see, both emission probability and transition probability are given. | ||
| + | <pre>[Emission probability] | ||
| + | Fair: 1/6 1/6 1/6 1/6 1/6 1/6 | ||
| + | Loaded: 0.1 0.1 0.1 0.1 0.1 0.5 | ||
| + | |||
| + | [Transition probability] | ||
| + | F -> F : 0.95 | ||
| + | F -> L : 0.05 | ||
| + | L -> L : 0.90 | ||
| + | L -> F : 0.10</pre> | ||
---- | ---- | ||
[[Category:CH391L]] | [[Category:CH391L]] | ||
Revision as of 11:26, 19 February 2011
Viterbi Algorithm
This is an 'dishonest casino' example from Durbin, et al. 'Biological Sequence Analysis' book. A casino used two types of dice: one is a 'fair' one that has equal chance to all six numbers, and the other is a 'loaded' one that has high chance of number 6 than the others. We have a sequence of dice numbers from the casino, and want to estimate when a dealer exchanged the dice.
We assume that the Hidden Markov Model of this example as below:
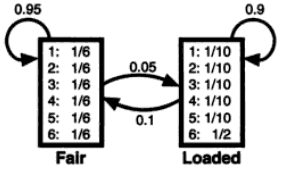
As you see, both emission probability and transition probability are given.
[Emission probability] Fair: 1/6 1/6 1/6 1/6 1/6 1/6 Loaded: 0.1 0.1 0.1 0.1 0.1 0.5 [Transition probability] F -> F : 0.95 F -> L : 0.05 L -> L : 0.90 L -> F : 0.10