CH391L/HiddenMarkovModel
Viterbi Algorithm
This is an 'dishonest casino' example from Durbin, et al. 'Biological Sequence Analysis' book. A casino used two types of dice: one is a 'fair' one that has equal chance to all six numbers, and the other is a 'loaded' one that has high chance of number 6 than the others. We have a sequence of dice numbers from the casino, and want to estimate when a dealer exchanged the dice.
We assume that the Hidden Markov Model of this example as below:
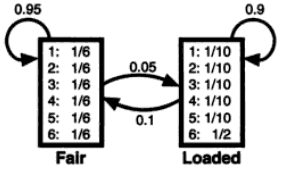
As you see, both emission probability and transition probability are given.
- [Emission probability]
- Fair: 1/6 1/6 1/6 1/6 1/6 1/6
- Loaded: 0.1 0.1 0.1 0.1 0.1 0.5
- [Transition probability]
- F -> F : 0.95
- F -> L : 0.05
- L -> L : 0.90
- L -> F : 0.10
Assume that we observed the following numbers from the casino: 22653245666
There is no 'begin' state in our model, so we will start our calculation at the second observation (this is the first order HMM, meaning that we need a 'previous state/observation').
First observation '2' has two probability: 0.167 if it was 'Fair' state, and 0.1 if it was 'Loaded' state.
To be continued...
HMMER
This is the most famous HMM application in biology. Developed by Sean Eddy (the author of many 'primer' series used in our class, and one of co-authors of 'Biological Sequence Analysis' textbook). Many 'sequence-based' domain information is originated from the database called Pfam, and this program is a core of Pfam construction. Also, the program is very mature, well-documented, so you can easily make your own 'profile family' when you have multiple sequence alignments.
General HMM libraray
- http://cran.r-project.org/web/packages/HMM/index.html (R statistical language)
- http://ghmm.org/ (C library)
- http://www.mathworks.com/help/toolbox/bioinfo/ref/hmmprofstruct.html (MATLAB Bioinfo toolbox)